I recently solved a coding challenge that required me to find all prime numbers up to a given number. I came up with a brute force solution first to get things working and get the brain juices flowing. Then I made some tweaks to make some improvements on the time complexity. Finally, I did some research to find an even better solution. I found the Sieve of Eratosthenes algorithm, which is an ancient algorithm for finding prime numbers. In this post, we'll go over how it works and how to implement it in JavaScript.

The first thing I did was come up with a brute force solution. I started by iterating over all numbers from 2 to the given number and checking if each number was divisible by any number less than it. If it was, then it was not a prime number and I skipped it. If it wasn't divisible by any number less than it, then it was a prime number and I added it to the final array.

This one isn't very efficient due to the nested loops (having a time complexity of O(n^2)), but it's a good starting point to understand the problem.

1function bruteForceGetPrimes(n) {
2  const primes = [];
3
4  for (let i = 2; i <= n; i++) {
5    let isPrime = true;
6
7    for (let j = 2; j < i; j++) {
8      if (i % j === 0) {
9        isPrime = false;
10        break;
11      }
12    }
13
14    if (isPrime) {
15      primes.push(i);
16    }
17  }
18
19  return primes;
20}

After getting the brute force solution working, I started thinking about how I could make it more efficient. I realized that I didn't need to check if a number was divisible by every number less than it. I only needed to check if it was divisible by prime numbers less than it. For example, I don't need to check if a number is divisible by 4 if I've already checked if it's divisible by 2 (since 4 is divisible by 2). So I created an array of prime numbers and checked if each number from 2 to upperBound was divisible by any of those prime numbers. If it was, then it was not a prime number and I excluded it from the array. If it wasn't divisible by any of those prime numbers, then it was a prime number and I added it to the array. Then I filtered the array of prime numbers to only include numbers greater than or equal to lowerBound.

This one is a little better because the nested loop (primes.some) iterates over fewer numbers and even exits the loop early as soon as it finds a prime that divides evenly into the current number. So not quite O(n), but better than O(n^2).

1function firstOptimizationGetPrimes({upperBound, lowerBound = 0}) {
2  if (upperBound < lowerBound || upperBound < 2) {
3    return [];
4  }
5
6  const primes = [];
7
8  for (let i = 2; i < upperBound; i++) {
9    if (i === 2) {
10        primes.push(i);
11    } else {
12      const isNotPrime = primes.some(prime => i % prime === 0)
13      
14      if (!isNotPrime) {
15        primes.push(i);
16      }
17    }
18  }
19
20  return primes.filter(prime => prime >= lowerBound);
21};

After coming up with my own brute force solution and iterating on it to make some optimizations, I did some research to see if there was an even better way to do it. I found the Sieve of Eratosthenes algorithm, which is an ancient algorithm for finding prime numbers. It's a very simple algorithm, but it's also pretty efficient.

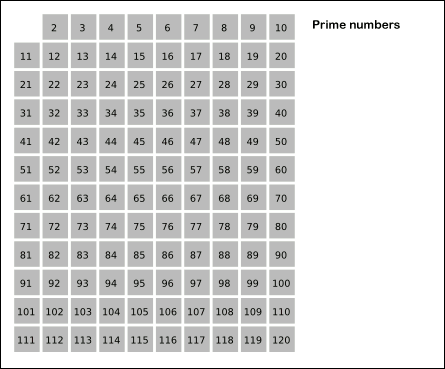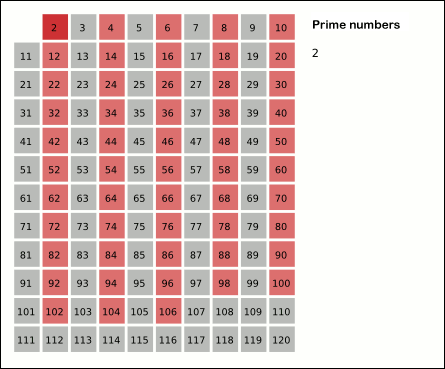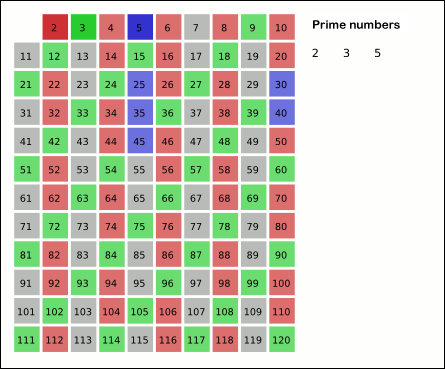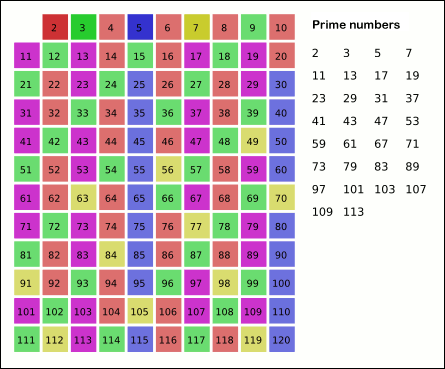
Essentially, the algorithm works by starting with a list of all numbers from 2 to the given number (because 0 and 1 are not prime). Then, starting with 2, it removes all multiples of 2 from the list. Then it moves on to 3, and removes all multiples of 3 from the list. It skips 4 because 4 has already been removed as a multiple of 2. So it goes on to 5 and continues this process until it reaches the given number. The numbers that are left in the list are all prime numbers.

So rather than checking the divisibility of each number in the given range by each number less than it, we can just remove all multiples of each prime number in the given range. This is more efficient because we only have to check divisibility by prime numbers, which are fewer in number than all numbers less than the given number.

Using JavaScript (because I'm a frontend gal), an implementation of this algorithm might look something like this:

1function regularSieveGetPrimes(n) {
2  // Create a boolean array of length n + 1 and initialize all entries as `true`
3  // (where each index represents a number)
4  // We start by assuming all numbers are prime
5  // If a number is proven to NOT be prime, we set its value to `false`
6  const primeBools = Array.from({ length: n + 1 }, (_, i) => true);
7
8  // start at 2 since we know 0 and 1 are not prime
9  for (let potentialPrime = 2; potentialPrime * potentialPrime <= n; potentialPrime++) {
10    // If `prime[potentialPrime]` is truthy, then it is a prime
11    if (primeBools[potentialPrime]) {
12      // Update all multiples of `potentialPrime` to be `false` (aka not prime)
13      for (let primeMultiple = potentialPrime * potentialPrime; primeMultiple <= n; primeMultiple += potentialPrime) {
14        primeBools[primeMultiple] = false;
15      }
16    }
17  }
18
19  // extract the primes from our boolean array
20  const primes = [];
21
22  // start at 2 since we know 0 and 1 are not prime
23  for (let i = 2; i <= n; i++) {
24    if (primeBools[i] === true) {
25      primes.push(i);
26    }
27  }
28
29  return primes;
30}

The first thing we do is create an array to keep track of the "primeness" of our numbers. We initialize this array to be the length of the given number plus one. Each index in this array represents a number from 0 to the given number. So we add 1 to the length because we want to include the given number in our array since array indices start at 0. And finally, all values in this array are initialized to true because we assume that all numbers are prime until proven otherwise.

Fun fact: a non-prime number is called a composite number.

const primeBools = Array.from({ length: n + 1 }, (_, i) => true);

Now that we have our array of booleans, we can start checking the numbers. Remember, with this algorithm we are "flagging" which numbers composite, or not prime, by determing which numbers are multiples of primes. We can do this by using nested loops.

For the outer loop, we want to check every number between 2 and the given number, incrementing by 1. We start at 2 because 2 is the first prime number. And instead of iterating all the way up to the given number, we just need to go up enough to reach the square root of the given number. This is because the square root of the given number is the largest possible prime factor of the given number (remember, a prime factor is a prime number that can perfectly divide the given number). So we don't need to check any numbers larger than the square root of the given number because everything larger that is not prime will have already been flagged by a smaller prime number.

For example, if the given number n is 49 (whose square root is 7), we only need to check up to 7 because 7 is the largest possible prime factor of 49. We don't need to worry about larger prime numbers (like 11, 13, 17, etc.) because they can't be prime factors of 49. And with this algorithm, we're only concerned with flagging which numbers are NOT prime. So any non-prime number larger than the square root of the given number will have already been flagged as not prime by a smaller prime number. In our example here, 8 will have been flagged by 2, 9 by 3, 10 by 2, 12 by 2, 14 by 2, 15 by 3, etc. So we don't need to keep checking past 7.

Going back to our code, if our current number, potentialPrime, is prime (or true in our primeBools array), we loop through all of its multiples in our inner loop and set them to false in our boolean array (we'll do this in a second). For example, if potentialPrime is 5, we can mark all multiples of 5 (10, 15, 20, etc.) as not prime.

1for (let potentialPrime = 2; potentialPrime * potentialPrime <= n; potentialPrime++) {
2  // If `prime[potentialPrime]` is truthy, then it is a prime
3  if (primeBools[potentialPrime]) {
4    // we'll do our inner loop here
5  }
6}

For our inner loop, we start at the square of potentialPrime because all of the multiples of potentialPrime that are less than its square have already been marked as false in our boolean array. For example, if potentialPrime is 3, we start our inner loop at 9 (the square of 3) because 6, while being a multiple of 3, has already been marked as false in our boolean array when potentialPrime was at 2 (since 6 is also a multiple of 2).

1// Update all multiples of `potentialPrime` to be `false` (aka not prime)
2for (let primeMultiple = potentialPrime * potentialPrime; primeMultiple <= n; primeMultiple += potentialPrime) {
3  primeBools[primeMultiple] = false;
4}

Finally, we loop through our boolean array and push the index of all of the true values to a new array (since all false values are composite/not prime). This new array will contain all of the prime numbers up to the given number.

1const primes = [];
2
3// start at 2 since we know 0 and 1 are not prime
4for (i = 2; i <= n; i++) {
5  if (primeBools[i] == true) {
6    primes.push(i);
7  }
8}
9
10return primes;

So putting it all back together, our function looks like this:

1function regularSieveGetPrimes(n) {
2  // Create a boolean array of length n + 1 and initialize all entries as `true`
3  // (where each index represents a number)
4  // We start by assuming all numbers are prime
5  // If a number is proven to NOT be prime, we set its value to `false`
6  const primeBools = Array.from({ length: n + 1 }, (_, i) => true);
7
8  // start at 2 since we know 0 and 1 are not prime
9  for (let potentialPrime = 2; potentialPrime * potentialPrime <= n; potentialPrime++) {
10    // If `prime[potentialPrime]` is truthy, then it is a prime
11    if (primeBools[potentialPrime]) {
12      // Update all multiples of `potentialPrime` to be `false` (aka not prime)
13      for (let primeMultiple = potentialPrime * potentialPrime; primeMultiple <= n; primeMultiple += potentialPrime) {
14        primeBools[primeMultiple] = false;
15      }
16    }
17  }
18
19  // extract the primes from our boolean array
20  const primes = [];
21
22  // start at 2 since we know 0 and 1 are not prime
23  for (let i = 2; i <= n; i++) {
24    if (primeBools[i] === true) {
25      primes.push(i);
26    }
27  }
28
29  return primes;
30}

The time complexity of this algorithm is O(n log log n), despite having nested loops. Let's break down the complexity of each part of the algorithm:

1. The outer loop runs for each number from 2 to the square root of n. So the number of iterations for the outer loop is approximately sqrt(n).
2. The inner loop marks multiples of the current prime number as not prime. So the number of iterations for the inner loop is roughly n divided by the current prime number.

Based on that, you would think that the time complexity would be O(n * sqrt(n)). However, the inner loop's iterations decrease as the algorithm progresses. So the overall number of operations is actually less than n * sqrt(n) since there is a decreasing number of iterations in the inner loop as the algorithm flags multiples of primes. As primes are found and multiples are flagged, the inner loop's iterations decrease, in a way explained by the mathematical concept of harmonic series, resulting in the time complexity of O(n log log n).

The space complexity is O(n), because we create an array of booleans that is the length of the given number. The amount of space needed is directly proportional to the size of the given number.

We won't get any more in-depth about the time and space complexity of this algorithm or Harmonic Series in this post, but if you're interested in learning more, check out the Wikipedia article on the Sieve of Eratosthenes.

While being pretty efficient in terms of time complexity, we can make it more efficient in terms of space complexity. If we are trying to find all of the prime numbers in a massive range, we don't want to have to worry about memory issues from creating an array that is the entire length of that range.

One solution to this is to use a segmented sieve. This is a variation of the Sieve of Eratosthenes that uses a smaller array to find the primes up to the square root of the given number. Then it uses this array to find the primes in the given range.

Here's what a JavaScript implementation might look like, with some slight modifications to allow specifying a range of numbers rather than just a single number:

// `getSmallPrimes` is an implementation of the Sieve of Eratosthenes algorithm, but using the square root of the upper bound as our limit
function getSmallPrimes(upperBound) {
    const primesArr = [];
    const limit = Math.sqrt(upperBound);
    const primesBoolArr = Array(Math.floor(limit) + 1).fill(true);
  // start at 2 since we know 0 and 1 are not prime
    for (let i = 2; i <= limit; i++) {
        if (primesBoolArr[i]) {
            for (let j = i * i; j <= limit; j += i) {
                primesBoolArr[j] = false;
            }
        }
    }
  // start at 2 since we know 0 and 1 are not prime
    for (let k = 2; k <= limit; k++) {
        if (primesBoolArr[k]) {
            primesArr.push(k);
        }
    }
    return primesArr;
}
// Segmented sieve implementation
function segmentedSieveGetPrimes({upperBound, lowerBound = 0}) {
    // `smallPrimes` has primes in range [2, sqrt(upperBound)]
    const smallPrimes = getSmallPrimes(upperBound);
    // Initializes an array `primesInRange` of boolean values, 
    // representing whether each number in the range [lowerBound, upperBound] is prime. 
    // Initially, all numbers are assumed to be prime.
    const primesInRange = Array(upperBound - lowerBound + 1).fill(true);
    for (let prime of smallPrimes) {
    // the first multiple of `prime` which is in range [lowerBound, upperBound] 
    // for example: 3's first multiple in range [28,40] is 30
        let lowerMultiple = Math.floor(lowerBound / prime);
        // If `lowerMultiple` is less than or equal to 1, 
        // set it to the first multiple of `prime` greater than or equal to `lowerBound`
        // If `lowerMultiple` is less than or equal to 1, 
        // it means the largest multiple found is less than `lowerBound`. 
        // In this case, we adjust it to the first multiple of `prime` that 
        // is greater than or equal to `lowerBound`.
        if (lowerMultiple <= 1) {
            lowerMultiple = prime + prime;
        } 
        // If `lowerBound` is not divisible by `prime`, 
        // adjust `lowerMultiple` to the next multiple of `prime` after `lowerBound`
        else if ((lowerBound % prime) !== 0) {
            lowerMultiple = (lowerMultiple * prime) + prime;
        } 
        // If `lowerBound` is divisible by `prime`, keep `lowerMultiple` as the first multiple of `prime` in the range `[lowerBound, upperBound]` (which in this case is the value of `lowerBound`)
        else {
            lowerMultiple = lowerMultiple * prime;
        }
        // marks multiples of `prime` as not prime in the range [low, high] 
        // by setting corresponding values in the `primesInRange` array to `false`
        for (let j = lowerMultiple; j <= upperBound; j = j + prime) {
            primesInRange[j - lowerBound] = false;
        }
    }
    const finalPrimesInRange = [];
  for (let i = lowerBound > 1 ? lowerBound : 2; i <= upperBound; i++) {
      if (primesInRange[i - lowerBound]) {
        finalPrimesInRange.push(i);
    }
  }
    return finalPrimesInRange;
}

The getSmallPrimes function is just an implementation of the Sieve of Eratosthenes algorithm that we built previously, returning an array of all prime numbers from 2 to the square root of the given upper bound number.

1// `getSmallPrimes` is an implementation of the Sieve of Eratosthenes algorithm, but using the square root of the upper bound as our limit
2function getSmallPrimes(upperBound) {
3    const primesArr = [];
4    const limit = Math.sqrt(upperBound);
5    const primesBoolArr = Array(Math.floor(limit) + 1).fill(true);
6
7  // start at 2 since we know 0 and 1 are not prime
8    for (let i = 2; i <= limit; i++) {
9        if (primesBoolArr[i]) {
10            for (let j = i * i; j <= limit; j += i) {
11                primesBoolArr[j] = false;
12            }
13        }
14    }
15
16  // start at 2 since we know 0 and 1 are not prime
17    for (let k = 2; k <= limit; k++) {
18        if (primesBoolArr[k]) {
19            primesArr.push(k);
20        }
21    }
22
23    return primesArr;
24}

We are using the square root of the upper bound as our limit instead of the upper bound itself (and adjusting the length of primesBoolArr accordingly). Remember, the reason we only need to find the primes up to the square root of the given number is because the multiples of all primes below the given number will be accounted for by the time we reach the square root of the given number. You can review the explanation of this logic in the outer loop section.

getSmallPrimes gets us all of the primes in the range [2, sqrt(upperBound)]. However, we want to find all of the primes in the range [lowerBound, upperBound]. In order to do that, we want to loop through each prime number that we found in the getSmallPrimes function. For each prime number, prime, we want to find all of the multiples of prime that are in the range [lowerBound, upperBound], starting with the smallest multiple of prime that is in that range (highlighted on lines 15-17 in the code block below).

For example, if we are trying to find all of the primes in the range [28, 40], and we are starting with the first prime number in our getSmallPrimes array (which is 2), we want to flag all of multiples of 2 that are in the range [28, 40]. The first multiple of 2 that is in that range is 28. So we want to start our loop at 28 when prime is 2. Then when prime is 3, we want to start our loop at 30, and so on.

1function segmentedSieveGetPrimes({upperBound, lowerBound = 0}) {
2  const smallPrimes = getSmallPrimes(upperBound);
3  const primesInRange = Array(upperBound - lowerBound + 1).fill(true);
4
5  for (let prime of smallPrimes) {
6    let lowerMultiple = Math.floor(lowerBound / prime);
7    if (lowerMultiple <= 1) {
8        lowerMultiple = prime + prime;
9    } else if ((lowerBound % prime) !== 0) {
10        lowerMultiple = (lowerMultiple * prime) + prime;
11    } else {
12        lowerMultiple = lowerMultiple * prime;
13    }
14
15    for (let j = lowerMultiple; j <= upperBound; j = j + prime) {
16        primesInRange[j - lowerBound] = false;
17    }
18  }
19
20  const finalPrimesInRange = [];
21  for (let i = lowerBound > 1 ? lowerBound : 2; i <= upperBound; i++) {
22    if (primesInRange[i - lowerBound]) {
23      finalPrimesInRange.push(i);
24    }
25  }
26  return finalPrimesInRange;
27}

Taking a look at the code, we initialize a lowerMultiple variable. We want the value of this variable to be the first multiple of prime that is in the range [lowerBound, upperBound].

If lowerBound is a multiple of prime, then lowerMultiple will be a nice integer. However, in the case that it is not, we are rounding down to the nearest integer.

let lowerMultiple = Math.floor(lowerBound / prime);

What if lowerMultiple is less than or equal to 1? This means that the lowerMultiple we have just calculated, while still being a multiple of prime, is actually below our lowerBound. Not what we want. So in this case, we want to adjust lowerMultiple to the first multiple of prime that is greater than or equal to lowerBound. We can do this by adding prime to the initially calculated lowerMultiple.

For example, if lowerBound is 2 and prime is 2, then lowerMultiple will be 1. In this case, lowerMultiple falls below our lowerBound, so we want to adjust it to the first multiple of prime that is greater than or equal to lowerBound. In this case, that would be 4.

if (lowerMultiple <= 1) {
  lowerMultiple = prime + prime;
}

If lowerMultiple is greater than 1 and lowerBound is NOT divisible by prime, then we want to adjust lowerMultiple to be the next multiple of prime after lowerBound. We can do this by multiplying lowerMultiple by prime and then adding prime.

For example, if lowerBound is 10 and prime is 3, lowerBound is NOT divisible by prime. lowerMultiple will come out to 3 (because we round down 10 divided by 3). So we want to adjust lowerMultiple to be the next multiple of prime after lowerBound (in this case, that would be 12). So lowerMultiple = (lowerMultiple * prime) + prime (or in this example, lowerMultiple = 3 * 3 + 3)

else if ((lowerBound % prime) !== 0) {
  lowerMultiple = (lowerMultiple * prime) + prime;
}

Otherwise, if lowerBound IS divisible by prime, then we want to keep lowerMultiple as the first multiple of prime in the range [lowerBound, upperBound] (which comes out to be the value of lowerBound, so you could just set it to lowerBound or just do lowerMultiple * prime).

else {
  lowerMultiple = lowerMultiple * prime;
}

In summary, we're grabbing the first multiple of prime that is in the range [lowerBound, upperBound] and setting it to lowerMultiple.

Now that we have our starting point for the inner loop with lowerMultiple, we can loop through all of the multiples of prime that are in the range [lowerBound, upperBound] and flag them as not prime in the primesInRange array.

We want to update the value at index [potentialPrime - lowerBound] because the length of primesInRange is only upperBound - lowerBound + 1. For example, if lowerBound is 28 and upperBound is 40, then the length of primesInRange is 13. This means that in primesInRange, the index of 28 is 0, the index of 29 is 1, the index of 30 is 2, and so on. So when potentialPrime is 30, we want to update the value at index 2 in primesInRange. This is why we subtract lowerBound from potentialPrime so that we update the value at the correct index.

for (let potentialPrime = lowerMultiple; potentialPrime <= upperBound; potentialPrime = potentialPrime + prime) {
  primesInRange[potentialPrime - lowerBound] = false;
}

With all of the non-prime numbers flagged in the primesInRange array, we can now loop through the primesInRange array and push all of the primes in the range [lowerBound, upperBound] to the finalPrimesInRange array.

Again, since the length of primesInRange is upperBound - lowerBound + 1, we want to adjust the index of the value that we are looking at in primesInRange by subtracting lowerBound from i.

const finalPrimesInRange = [];
for (let i = lowerBound; i <= upperBound; i++) {
  if (primesInRange[i - lowerBound]) {
    finalPrimesInRange.push(i);
  }
}
return finalPrimesInRange;

So putting it all back together, our functions look like this:

// `getSmallPrimes` is an implementation of the Sieve of Eratosthenes algorithm, but using the square root of the upper bound as our limit
function getSmallPrimes(upperBound) {
    const primesArr = [];
    const limit = Math.sqrt(upperBound);
    const primesBoolArr = Array(Math.floor(limit) + 1).fill(true);
  // start at 2 since we know 0 and 1 are not prime
    for (let i = 2; i <= limit; i++) {
        if (primesBoolArr[i]) {
            for (let j = i * i; j <= limit; j += i) {
                primesBoolArr[j] = false;
            }
        }
    }
  // start at 2 since we know 0 and 1 are not prime
    for (let k = 2; k <= limit; k++) {
        if (primesBoolArr[k]) {
            primesArr.push(k);
        }
    }
    return primesArr;
}
// Segmented sieve implementation
function segmentedSieveGetPrimes({upperBound, lowerBound = 0}) {
    // `smallPrimes` has primes in range [2, sqrt(upperBound)]
    const smallPrimes = getSmallPrimes(upperBound);
    // Initializes an array `primesInRange` of boolean values, 
    // representing whether each number in the range [lowerBound, upperBound] is prime. 
    // Initially, all numbers are assumed to be prime.
    const primesInRange = Array(upperBound - lowerBound + 1).fill(true);
    for (let prime of smallPrimes) {
    // the first multiple of `prime` which is in range [lowerBound, upperBound] 
    // for example: 3's first multiple in range [28,40] is 30
        let lowerMultiple = Math.floor(lowerBound / prime);
        // If `lowerMultiple` is less than or equal to 1, 
        // set it to the first multiple of `prime` greater than or equal to `lowerBound`
        // If `lowerMultiple` is less than or equal to 1, 
        // it means the largest multiple found is less than `lowerBound`. 
        // In this case, we adjust it to the first multiple of `prime` that 
        // is greater than or equal to `lowerBound`.
        if (lowerMultiple <= 1) {
            lowerMultiple = prime + prime;
        } 
        // If `lowerBound` is not divisible by `prime`, 
        // adjust `lowerMultiple` to the next multiple of `prime` after `lowerBound`
        else if ((lowerBound % prime) !== 0) {
            lowerMultiple = (lowerMultiple * prime) + prime;
        } 
        // If `lowerBound` is divisible by `prime`, keep `lowerMultiple` as the first multiple of `prime` in the range `[lowerBound, upperBound]` (which in this case is the value of `lowerBound`)
        else {
            lowerMultiple = lowerMultiple * prime;
        }
        // marks multiples of `prime` as not prime in the range [low, high] 
        // by setting corresponding values in the `primesInRange` array to `false`
        for (let j = lowerMultiple; j <= upperBound; j = j + prime) {
            primesInRange[j - lowerBound] = false;
        }
    }
    const finalPrimesInRange = [];
  for (let i = lowerBound > 1 ? lowerBound : 2; i <= upperBound; i++) {
      if (primesInRange[i - lowerBound]) {
        finalPrimesInRange.push(i);
    }
  }
    return finalPrimesInRange;
}

The time complexity of this segmented Sieve of Eratosthenes algorithm is the same as a regular Sieve of Eratosthenes algorithm, which is O(n log log n).

The space complexity is reduced to O(sqrt(n)) since we aren't storing every single number in the range. This is a nice improvement on the space complexity of a regular Sieve of Eratosthenes algorithm, which is O(n). However, this will still hit memory limitations for extremely large ranges due to the array of booleans that we are creating.

We can take our segmented Sieve of Eratosthenes algorithem one step further by partitioning the range into smaller chunks. This will reduce the space complexity even further, but will increase the time complexity slightly due to an added loop.

First, let's modify getSmallPrimes a bit to make it more reusable. We'll rename it to getPrimes and have it accept a num parameter. We'll assume that num is already the integer that you want for the upper bound. This allows us to eliminate the limit variable. I've highlighted the changed lines below:

1// `getPrimes` is an implementation of the Sieve of Eratosthenes algorithm
2function getPrimes(num) {
3    const primesArr = [];
4    const primesBoolArr = Array(num + 1).fill(true);
5
6  // start at 2 since we know 0 and 1 are not prime
7    for (let i = 2; i <= num; i++) {
8        if (primesBoolArr[i]) {
9            for (let j = i * i; j <= num; j += i) {
10                primesBoolArr[j] = false;
11            }
12        }
13    }
14
15  // start at 2 since we know 0 and 1 are not prime
16    for (let k = 2; k <= num; k++) {
17        if (primesBoolArr[k]) {
18            primesArr.push(k);
19        }
20    }
21
22    return primesArr;
23}

Then we'll break the logic for the segmented Sieve of Eratosthenes algorithm into its own function so that we can call it for each chunk of the range. This is the same as the getPrimes function we had in our first segmented sieve implementation, but we've removed the smallPrimes calculation and are now passing it in as a parameter.

1function segmentedSieve({upperBound, lowerBound = 0, smallPrimes}) {
2    // Initializes an array `primesInRange` of boolean values, 
3    // representing whether each number in the range [lowerBound, upperBound] is prime. 
4    // Initially, all numbers are assumed to be prime.
5    const primesInRange = Array(upperBound - lowerBound + 1).fill(true);
6
7    for (let prime of smallPrimes) {
8    // the first multiple of `prime` which is in range [lowerBound, upperBound] 
9    // for example: 3's first multiple in range [28,40] is 30
10    let lowerMultiple = Math.floor(lowerBound / prime);
11
12        // If `lowerMultiple` is less than or equal to 1, 
13        // set it to the first multiple of `prime` greater than or equal to `lowerBound`
14        // If `lowerMultiple` is less than or equal to 1, 
15        // it means the largest multiple found is less than `lowerBound`. 
16        // In this case, we adjust it to the first multiple of `prime` that 
17        // is greater than or equal to `lowerBound`.
18        if (lowerMultiple <= 1) {
19            lowerMultiple = prime + prime;
20        } 
21
22        // If `lowerBound` is not divisible by `prime`, 
23        // adjust `lowerMultiple` to the next multiple of `prime` after `lowerBound`
24        else if ((lowerBound % prime) !== 0) {
25            lowerMultiple = (lowerMultiple * prime) + prime;
26        } 
27
28        // If `lowerBound` is divisible by `prime`, keep `lowerMultiple` as the first multiple of `prime` in the range `[lowerBound, upperBound]` (which in this case is the value of `lowerBound`)
29        else {
30            lowerMultiple = lowerMultiple * prime;
31        }
32
33        // marks multiples of `prime` as not prime in the range [low, high] 
34        // by setting corresponding values in the `primesInRange` array to `false`
35        for (let j = lowerMultiple; j <= upperBound; j = j + prime) {
36            primesInRange[j - lowerBound] = false;
37        }
38    }
39
40    const finalPrimesInRange = [];
41  for (let i = Math.max(2, lowerBound); i <= upperBound; i++) {
42      if (primesInRange[i - lowerBound]) {
43        finalPrimesInRange.push(i);
44    }
45  }
46
47    return finalPrimesInRange;
48}

Finally, we'll create a new getPrimesInRange function. This function gets all of the small primes in the range [2, sqrt(upperBound)], just like how we previously did in the original getPrimes function. Then we divide the range [Math.max(2, lowerBound), upperBound] into smaller segments of size sqrt(upperBound). For each of these segments, we call the segmentedSieve function to find all of the primes in that segment. We then append these primes to the doubleSegmentedSieveGetPrimes array and return it.

1function doubleSegmentedSieveGetPrimes({upperBound, lowerBound = 0}) {
2  const sqrtUpperBound = Math.floor(Math.sqrt(upperBound));
3  // `getPrimes` has primes in range [2, sqrtUpperBound]
4    const smallPrimes = getPrimes(sqrtUpperBound);
5
6   /*
7  divide the range [Math.max(2, lowerBound), upperBound] into
8  smaller segments of size sqrtUpperBound,
9  use segmentedSieve to find all the
10  primes in the segment range [l, r] and append
11  to allPrimesInRange
12  */
13  const allPrimesInRange = [];
14  
15  for (let i = Math.max(2, lowerBound); i <= upperBound; i += sqrtUpperBound) {
16    const upper = Math.min(i + sqrtUpperBound - 1, upperBound);
17    allPrimesInRange.push(...segmentedSieve({upperBound: upper, lowerBound: i, smallPrimes}));
18  }
19
20  return allPrimesInRange;
21}

If you're curious as to just how much faster the segmented Sieve of Eratosthenes algorithm is from the regular one, you can use JavaScript's performance.now() method to check the execution time of each algorithm.

You could use Date.now() instead, but I opted for performance.now(). While Date.now() is faster, it is only accurate to ~1ms, whereas performance.now() is accurate to the microsecond. Depending on the size of the range that you are checking, performance.now() can give you a more accurate representation of the execution time. You can read more about it on the MDN docs.

function checkExecutionTime(cb) {
  const t0 = performance.now();
  cb();
  const t1 = performance.now();
  console.log(`Call took ${t1 - t0} milliseconds.`);
}
// Brute force
checkExecutionTime(() => bruteForceGetPrimes(100000));
// My first optimization
checkExecutionTime(() => firstOptimizationGetPrimes({ upperBound: 100000, lowerBound: 0 }));
// Regular Sieve of Eratosthenes
checkExecutionTime(() => regularSieveGetPrimes(100000));
// Segmented Sieve of Eratosthenes
checkExecutionTime(() => segmentedSieveGetPrimes({ upperBound: 100000, lowerBound: 0 }));
// "Doubly" segmented Sieve of Eratosthenes
doubleSegmentedSieveGetPrimes(() => getPrimes({ upperBound: 100000, lowerBound: 0 }));

Here are the results of the above code to check the execution time of each algorithm for a range of [0, 100000]:

• Brute force algorithm - 1346.300000011921 milliseconds
• First optimization - 150.29999995231628 milliseconds
• Regular Sieve of Eratosthenes algorithm - 4.900000035762787 milliseconds
• Segmented Sieve of Eratosthenes algorithm - 1.0999999642372131 milliseconds
• "Doubly" segmented Sieve of Eratosthenes algorithm - 1.699999988079071 milliseconds

As you can see, the segmented Sieve of Eratosthenes algorithm is the fastest of all 5 solutions. The "doubly" segmented Sieve of Eratosthenes is tad slower due to the extra looping to partition the range into smaller segments. And the regular Sieve of Eratosthenes algorithm is the slowest of the three sieves. However, all three sieves are much faster than the brute force algorithm and my first optimization.

To recap, the Sieve of Eratosthenes algorithm is a way to find all prime numbers up to a given number. It works by starting with a list of all numbers up to the given number, and then removing all multiples of each number in the list. The numbers that are left are prime numbers.

In a segmented sieve, we use the Sieve of Eratosthenes algorithm, but we only store the primes up to the square root of the upper bound. We then use those primes to find the primes in the range [lowerBound, upperBound]. This reduces the space complexity of the algorithm from O(n) to O(sqrt(n)) to make it more memory efficient.

If we want to further optimize the space complexitiy of the segmented sieve, we can partition the range [lowerBound, upperBound] into smaller segments of size sqrt(upperBound). We can then use the segmented sieve to find the primes in each of these segments. This reduces the space complexity of the algorithm, but also slightly increases the time complexity.